第30课 背包问题

解决了汉诺塔的问题之后，本章我们再来解决一个背包问题。背包问题是动态规划算法的经典问题。

动态规划与分治法类似，都是把大的问题拆分成小的问题，通过寻找大问题与小问题之间的关系，解决一个个小问题，最终达到解决大问题的目的。但不同的是，分治法中的子问题和子子问题在形式上是一样的，同样的计算被重复地执行了很多次；而动态规划则要记住每一步的子问题答案，然后将这些答案带到新的问题中，所以我们可以认为用动态规划解决问题的核心就在于填表，表填写完毕，最优解也就找到了。

好了，现在回到背包问题，我们来举例说明。假设这里有4本书，分别重200g、300g、400g和500g。4本书的价格分别为30元、40元、60元和50元。我们的背包只能装800g的书，那我们应该选哪几本书才能够让背包内的书的总价最高呢？

首先在Scratch中创建4个列表，对应4本书，通过列表左下角的加号为每个列表添加内容，列表中的第一项表示书的重量，第二项表示书的价格。完成后如图30-1所示。

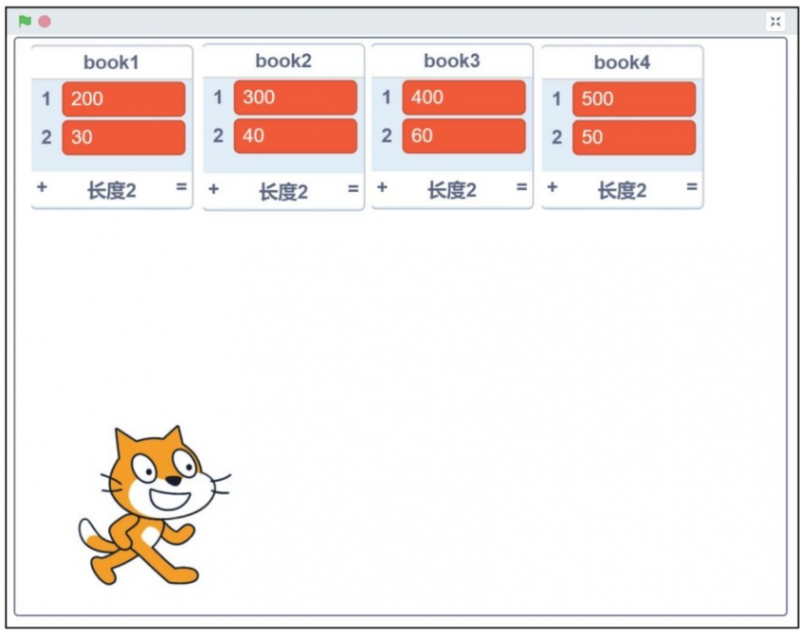
图30-1 创建4个列表，对应4种书

用动态规划的方法解决背包问题就是一本书一本书地放，不但是一本一本地放，而且还要把背包分成一个个小背包，因为我们的书都是以100g为单位的，背包总共能装800g的书，所以这里就把背包分为8个状态。对于只有第一本书的情况，我们要把这8种状态下的最优解都找到。同样创建一个列表用来保存对应的数据，如图30-2所示。

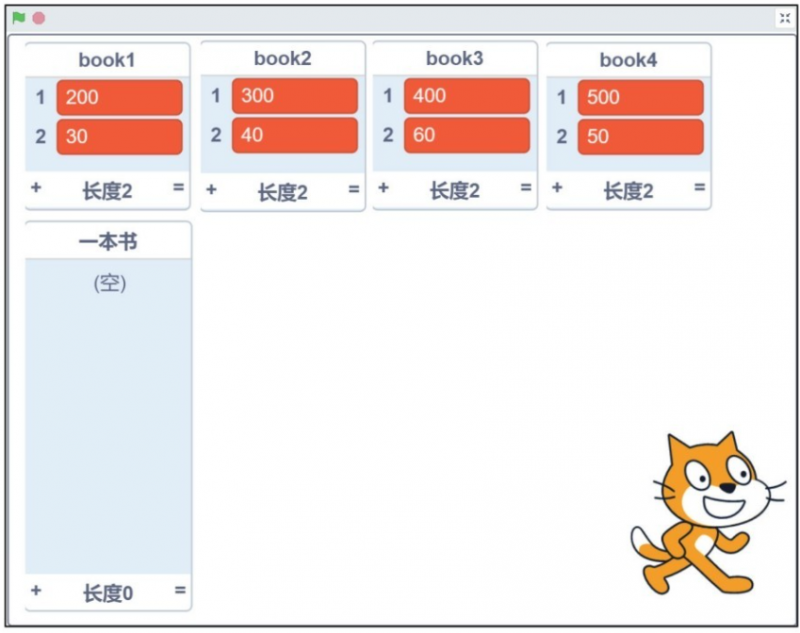
图30-2 创建1个列表存放只有第一本书的情况

在只有第一本书的情况下，我们只需要考虑它是不是能够装到对应的小背包里，所以寻找最优解对应的程序如图30-3所示。

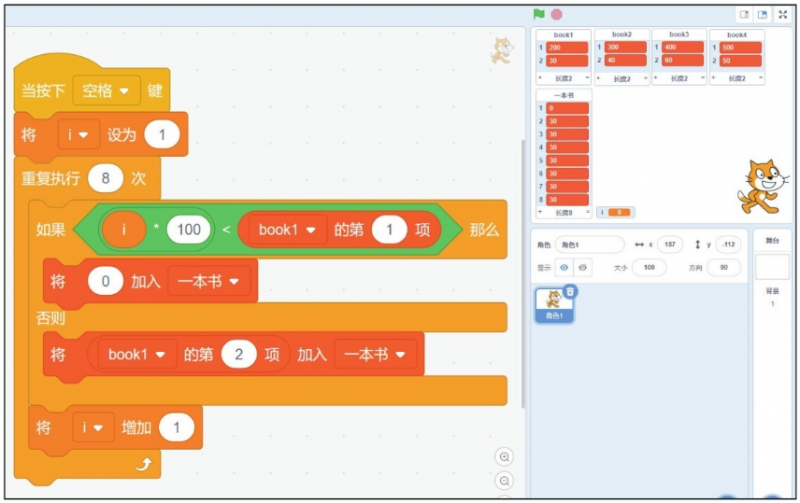
图30-3 只有第一本书的对应程序

这里新建了一个变量“i”来保存循环的次数，每次都会比较小背包与第一本书的重量，如果小背包装不下第一本书，则将0加入列表；如果小背包能装下第一本书，则将第一本书的价格加入列表。程序按下空格键的时候运行，此时我们能看到只有第一项的数字为0，这是因为这个状态下背包只能装100g的书，所以第一本书放不进去，因此价格为0。

接着来看两本书的情况，同样要新建一个列表。对于这个列表中的数据填写规则描述如下。

（1）判断第二本书是不是能够单独放在小背包里，如果不能就将前一个列表中的对应数据放到这个列表中。

（2）如果第二本书能够单独放在小背包里，那么就要看看小背包能不能放下两本书，如果不能就再比较前一个列表中的值与第二本书的价格，把大数填到第二个列表中。

（3）如果能放下两本书，那直接就把第二本书放进去就可以了。

对应的程序如图30-4所示。

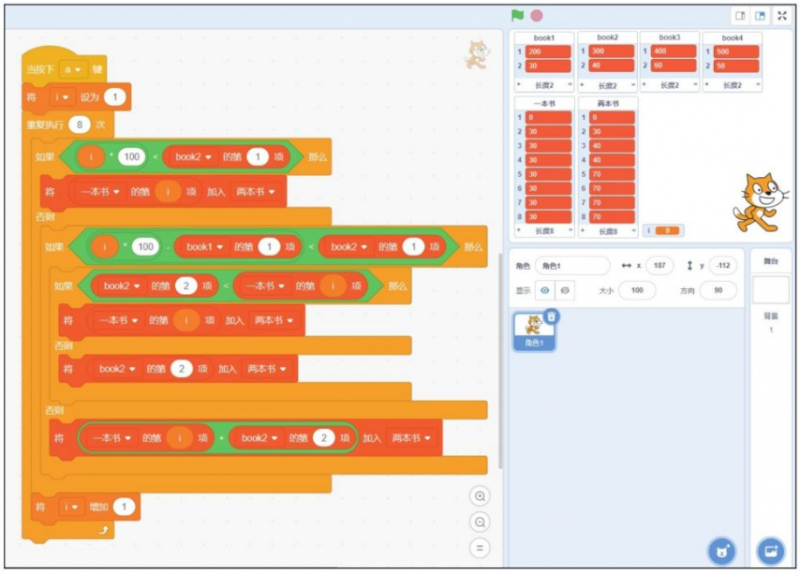
图30-4 两本书对应的程序

按下键盘上的a键运行程序。我们看到第3个数变成了40，说明在小背包限重在300g的时候能放下第二本书了，而第二本比第一本书的价格高，所以这个小背包里放的是第二本书。之后的第5个数变成了70，说明此时能放下两本书了。

再接下来看看放3本书的情况，依然要新建一个列表。对于这个列表中的数据填写规则和两本书的时候很像，具体描述如下。

1）判断第三本书是不是能够单独放在小背包里，如果不能，就将前一个列表中的对应数据放到这个列表中。

2）如果第三本书能够单独放在小背包里，那么就再看看小背包能不能同时放下3本书，如果可以，就直接放3本书。

3）如果不能同时放下3本书，那么就要分成两种情况：

（a）不放第三本书，这样可以直接取前一个列表中的对应数据；

（b）放第三本书，然后把这个问题变成在剩余的重量限制下寻找最优解的问题。

再比较（a）和（b）的结果，选出价格高的情况。

（a）情况下的函数如图30-5所示。

图30-5 （a）情况的函数

这里为了让程序更加直观，我们新建了一个变量“三本书a的数据”。对应（b）情况下的函数如图30-6所示。